Google des Tages: 8 / 2(2 + 2) ein virales Mathematik-Problem – Google löst es korrekt

Google des Tages: 8/2(2+2) (?)
Mal etwas spaßiges und vielleicht für einige auch sehr kniffliges zum Wochenende: Obige Mathematik-Aufgabe kursiert seit einigen Tagen im Web und ist als mathematisches Problem viral gegangen. Der Grund ist ganz einfach, dass es – so meinen es zumindest die selbsternannten Experten – zwei mögliche Lösungen gibt, die jede Gruppe ausgiebig verteidigt. Deswegen befragen wir einfach mal Professor Google und machen es zum „Google des Tages“, denn der in der Suchmaschine integrierte Taschenrechner löst diese Aufgabe glücklicherweise korrekt.
Über Mathematik kann man eigentlich nicht streiten, da sie auf einfachen Regeln (Ich weiß, das ist Ansichtssache) basiert, die vollkommen logisch sind. Natürlich gibt es Aufgaben mit Ergebnismengen, in denen mehrere Lösungen richtig sein können – allerdings nur dann, wenn Variablen zum Einsatz kommen. Aber die folgende kurze Mathematik-Aufgabe bringt tatsächlich viele Menschen zum Verzweifeln und führt zu angestrengten Diskussionen.
Es sieht nach einer sehr leichten Aufgabe aus, denn es sind nur vier Zahlen enthalten, mit denen jeder auch ohne Taschenrechner schnell zu einem Ergebnis kommen sollte. Das Problem ist allerdings, dass man natürlich nicht von Links nach Rechts rechnen darf, sondern die in der Mathematik festgelegte Reihenfolge einhalten muss. Und genau diese Reihenfolge bringt die Menschen zum Verzweifeln und sorgt dafür, dass es drei mögliche Lösungen gibt, wovon zwei aber natürlich nicht den Rechenweg eingehalten haben.
Es kursieren die Lösungen 1 und 16, wobei beide vielleicht irgendwie nachvollziehbar sind, denn viele kennen die echte Grundreihenfolge nicht mehr. Es ist schon faszinierend wie viele verschiedene Herangehensweisen es an eine solch kurze und eigentlich simple Aufgabe gibt.
Ergebnis 1
Zuerst wird die Klammer gelöst, sodass wir die Aufgabe 8/2(4) haben. Anschließend wird die Klammer aufgelöst, sodass noch 8/8 da steht, bei dem dann bekanntlich 1 herauskommt. Der Fehler liegt hier darin, dass nicht von Links nach Rechts gerechnet wurde, also FALSCH.
Ergebnis 16
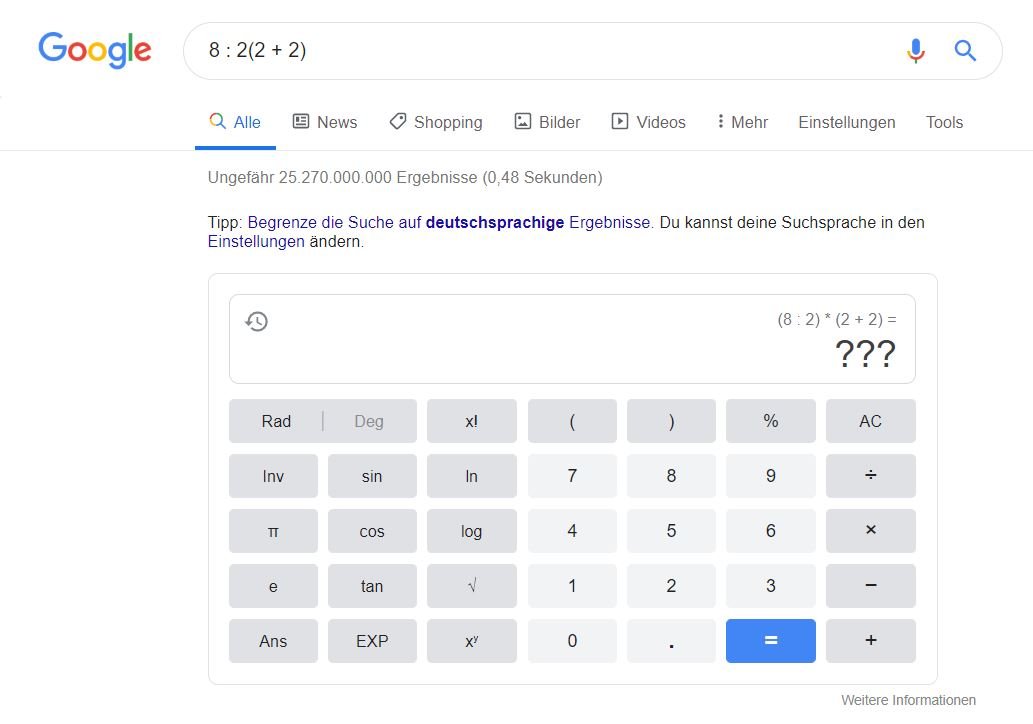
Es wird zuerst die Klammer gelöst, sodass wieder die Aufgabe 8/2(4) dort steht. Jetzt von links nach Rechts lösen und schon steht das Ergebnis 16 auf dem Display. Wichtig dabei ist, vor der Klammer steht das Multiplikationszeichen, das aber weggelassen werden darf. Das ist die einzige korrekte Lösung.
Glücklicherweise beachtet der in der Google Websuche integrierte Taschenrechner alle Regeln und zeigt das richtige Ergebnis an, denn sonst gäbe es wohl noch größere Diskussionen um die Lösung 16. Auch alle von mir getesteten Android-Taschenrechner zeigen das korrekte Ergebnis, aber die guten alten (billigen) Schul-Taschenrechner können durch ihre Syntax teilweise gar nicht anders lösen.
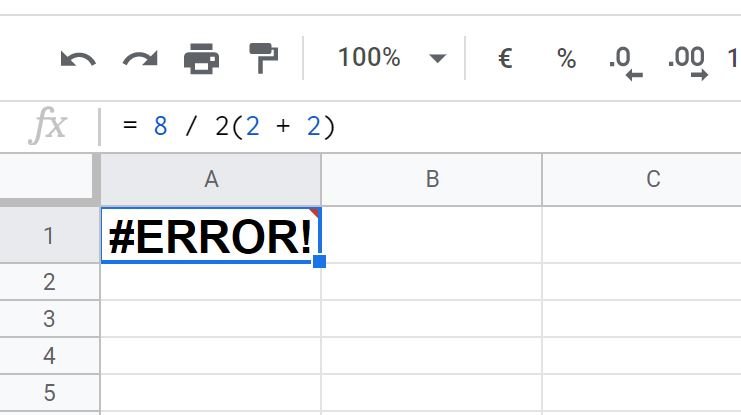
Und um wieder einmal den Kreis zu Google zu schließen: Ganz bitter wird es bei der Tabellenkalkulation Google Sheets: Diese steigt bei der Eingabe der Aufgabe einfach aus und zeigt nur einen Fehler an. Das liegt aber nicht daran, dass sich die Algorithmen nicht für eine Aufgabe entscheiden können, sondern daran, dass die App mit dem fehlenden Multiplikationszeichen vor der Klammer ein Problem hat. Gibt man dort stattdessen „8/2*(2+2)“ ein, dann erhält man auch dort die korrekte Lösung. Gottseidank.
So, und jetzt darf gerne diskutiert werden, ob es noch weitere „logische“ Lösungen gibt, ich zumindest habe keine weiteren gefunden. Gerne auch noch weitere solche Aufgaben in die Kommentare
Siehe auch
» Google Taschenrechner: Die Android-App zeigt Ergebnisse jetzt auch in Form von Brüchen
» 2 * 3 = 4: Der Taschenrechner in der Google Websuche erhält modernisiertes Design und einen Verlauf
Pixel 4 Leaks: Innovationen & Neue Technologien – alles was über Googles neue Smartphones bekannt ist
Google Assistant: Nachrichten aus WhatsApp, Telegram & Co. lassen sich jetzt vorlesen und beantworten
Smart Display Gratis: Saturn schenkt euch zu jedem Pixel 3a XL ein Google Nest Hub – für nur 449 Euro
GoogleWatchBlog bei Google News abonnieren | GoogleWatchBlog-Newsletter






meine güte, entfernt bitte die klammer um die 4. da gehört keine Klammer mehr hin da eine Klammer nur dafür da ist um den Inhalt zuerst auszurechnen und eine alleinstehende vier kann man nicht mehr ausrechnen. Es verwirrt so nur und ist optisch falsch.
https://www-watson-de.cdn.ampproject.org/v/s/www.watson.de/amp/!455318362?amp_js_v=a2&_gsa=1#referrer=https%3A%2F%2Fwww.google.com&_tf=Von%20%251%24s&share=https%3A%2F%2Fwww.watson.de%2Fwissen%2Ftwitter%2F455318362-mathe-dieses-raetsel-macht-gerade-alle-verrueckt-sogar-taschenrechner-verwirrt
Viel besser erklärt, das 1 nicht falsch ist, sondern auf alten Rechenregeln beruht.
Ist aber die falsche Erklärung.
In vielen technischen Fällen wird implizierte Multiplikation auch heute noch vor explizierter Multiplikation gelöst und in diesen Fächern gelten aber auch Regeln wie mathematische Therme aufgeschrieben werden dürfen und wie nicht und obige Formel ist nicht korrekt aufgeschrieben und daher eigentlich ungültig.
Wenn man 1 rausbekommt, liegt der Fehler mitnichten daran, dass man nicht von links nach rechts gerechnet hat. Bei Faktoren ist die Reihenfolge egal. Faktoren kann man vertauschen. Dass sich zwei mögliche Ergebnisse ergeben liegt einzig und allein an der dämlichen Schreibweise der Aufgabe. Wenn man diese mit einem „ordentlichen“ Bruchstrich geschrieben hätte, gebe es nur eine Lösung. So aber kann man „2(2+2)“ als zusammengehörig ansehen (wie, wenn eine Klammer gesetzt wurde) und dann ist das Ergebnis nämlich 1. Für mich als Mathematiker ist es also weniger ein Matheproblem als ein „Orthographieproblem“!
Das ist ganz grober Schwachsinn mit deiner alten Regel, 1war schon immer falsch, Mathe ist Logik und keine ansichtssache…
Heißer Schwachsinn ist es so einen Unsinn zuschreiben. Die Regeln sind bin Menschenhand geschrieben und nicht göttlich. Von daher die sie Veränderungen unterworfen. Und passen sich im Laufe Zeit an und werden angepasst.
Es gab Zeiten da galt die Eins als Prim.
Ok, wenn ich die Aufgabe mit „/“ und nicht mit „:“ oder „÷“ schreibe, dann ist die Antwort doch eindeutig und nur 1.
Das hier verwendete „/“ ist doch nur die einzeilige Darstellung eines Bruchs. Und wenn ich den Bruch ausschreibe, steht über dem Bruchstrich 8 und darunter 2(2+2). Ausgerechnet somit 8 über dem Bruchstrich, 8 darunter und das ergibt 1.
Die originale Darstellung ist mit einem „÷“, oder? Und dann ist’s 16.
Oder liege ich falsch?
Du bist falsch alter, es ist egal welches geteilt du verwendest, unter dem Bruchstrich steht dann nämlich nur 2. Nicht 2(2+2)!!!!! Du kannst nicht einfach die ganze Aufgabe unter einen Bruchstrich setzen, nur die zu teilende Zahl. Ich verstehe nicht wer auf die Idee kommt erst die Klammer Mal 2 zu nehmen, man muss schon sehr dumm sein soetwas zu tun, Mathe ist doch ganz einfache Logik, und keine Ansichtssache.
@Daniel: Division und Bruch ist das Gleiche nur anders geschrieben. Da man einzeilig nicht ausdrücken kann wie weit der Bruch geht, MUSS man da mit Klammern arbeiten um es auszudrücken. Der Bruch könnte ja auch nur bis über die erste 2 gehen und nicht über die Klammer… Deshalb ist ein / gleich zu behandeln wie ein ÷
Bruch und Division ist nicht dasselbe, weil man eben keine Klammern braucht.
Wenn man den Bruch untereinander schreibt braucht man keine Klammer, da hast du recht. Aber in einer Zeile nebeneinander geschrieben braucht man auch beim Bruch die Klammern.
Wie oben gepostet war es früher so, das erst Duell kannst aufgelöst wurde. Jetzt ist es aber anders, also strikt von links nach rechts.
Übrigens ging vor mehreren Jahren „6÷2(1+2)“ rum und da haben sich auch alle gestritten ob es nun 9 oder 1 ist. Es hilft also den meisten nicht ÷ statt / zu nutzen
Das kommt komplett darauf an, wie man das geteilt-zeichen interpretiert. Es ist nämlich nicht offensichtlich ob man 8/2 oder nur die 2 reinziehen muss. Es könnte 8 geteilt durch 2(2+2) sein, oder 8/2 (2+2). Mein wissenschaftlicher Taschenrechner interpretiert es als das erstere. Mit einem * zwischen der 2 und der Klammer als das Zweitere. Mit einem Bruch wäre es eindeutig. Genau das ist der Grund, warum die Rechnung viral ist.
Mathe hat klare Regeln, da gibt es keinen Interpretationsspielraum. Das ÷ ist eine einfache Division ohne Klammern, also gilt da einfach „Klammer vor Exponent vor Punkt vor Strich“ zudem gibt es die für Division (und Subtraction) die links Assoziativität.
Deshalb:
6÷2(1+2)
Klammer vor allem anderen auflösen:
= 6÷2*3
Wegen links Assoziativität zuerst die Division:
= 3*3
= 9
hier auch der Wikipedia Artikel für die Reihenfolge in der die Operatoren anzuwenden sind: https://de.wikipedia.org/wiki/Operatorassoziativit%C3%A4t
Absoluter quatsch es kann nur 1 herauskommen denn zuerst muss jede Zahl in der Klammer mit dem Multiplikator davor (Punkt vor strich) verrechnet werden danach wird immer die Klammer aufgelöst und danach wird erst dividiert wurden in den letzten 10 Jahren (so lange bin ich aus der Schule) die Mathematik regeln komplett erneuert
@Heiko: „Punkt vor Strich“ ist unvollständig und nur für Schüler die noch keine Klammern und Exponenten haben. Vollständig wäre es „Klammern vor Exponeten vor Punkt vor Strich“. Aber selbst wenn man es rein zieht wie du sagst, kommt 16 raus: 8/2(2+2) = (8/2*2+8/2*2) = 4*2+4*2 = 8+8 = 16
Man muss dann nämlich das komplette 8/2 rein ziehen und nicht nur die 2.
Rudi
Als Realschüler habe ich gelernt, dass ein Bruchstrich eine Klammer ersetzt! Also kommt 1 raus, da der Nenner erstaufgelöst werden muss! Also 8/(2(2+2)).
@Rudi: Wenn der Bruchstricht auch über das (2+2) mit drüber gehen würde, hättest du recht. Richtig geschrieben ist ein Bruchstrich ja auch nicht schräg sondern horrizontal und man sieht genau über was er geht. Da bei einem / aber nicht ersichtlich ist, über was er alles geht, ist er wie ein : zu behandeln und man muss Klammern setzen, wenn er über mehr gehen soll.
8÷2(2+2)=X | ×2(2+2)
8=2X(2+2) | Klammer ausmultiplizieren
8=4X+4X
8=8X | ÷8
1=X
wenn jemand einen mathematischen Fehler sieht gerne melden
Warum 16 falsch ist:
wenn ich z.B.:
8÷2(2+2)=X | Klammer ausmultiplizieren
8÷4+4=X | wenn man nun stumpf von links nach rechts rechnet kommt z.B. 6 heraus, das ist falsch! Selbst die die 16 als Lösung favorisieren werden mir Recht geben das 6 die falsche Lösung ist.
zur Begründung: die Aufgabe 8÷2(2+2)=X besteht aus drei Thermen 1.) 8; 2.) 2(2+2); 3.) X;
es gibt in der Mathematik keine Regel das eine Aufgabe von links nach rechts gerechnet werden muss! Eine Gleichung muss Term für Term gelöst werden und dabei muss immer der selbe Wert links und rechts des Gleichheitszeichens stehen.
8÷2(2+2)=16 ? wenn das so wäre dann wäre (2+2)8÷2=16 das hieße dann ich könnte da 16=16 ist auch schreiben (2+2)8÷2=8÷2(2+2) bei dieser Gleichung könnte man beide Seiten mit 3 multiplizieren so dass (2+2)8÷2=8÷2(2+2) nun könnte man die Klammern ausmultiplizieren so dass 16+16÷2=8÷4+4 und das ist (da ja Punkt vor Strichrechnung geht und Summanden vertauschbar sind) 16+8=2+4 was 24=6 ergibt.
Also alle die der Meinung sind dass die Lösung der o.g. Aufgabe gleich 16 ist, sind auch der Meinung dass 24 gleich 6 ist.
P.S. falls einer von Euch bei mir etwas Geld wechseln will immer gerne.
immer gerne.
Man rechnet doch immer erst den Inhalt der Klammern aus dann die möglichen Punkt- und danach die möglichen Strich-Rechnungen
@Kay Immig:
8÷2(2+2)=X | ×2(2+2) <– Der Streitpunkt ist ja ob das (2+2) bei der Bruchschreibweise mit unterm Bruch wäre oder nicht. Wenn es nicht unterm Bruchstrich ist (also Ergebnis 16), dann kommt das raus:
8÷2(2+2)(2+2)=(2+2)X
Du müsstest also wenn dann eher das machen:
8÷2(2+2)=X | ÷(2+2)
8÷2=X/(2+2)
4=X/4 | *4
16=X
und dazu:
8÷2(2+2)=X | Klammer ausmultiplizieren
8÷4+4=X | <– Wieder der Unterschied ob unterm Bruchstrich oder nicht… Wenn es nicht unterm Bruchstrich ist (also Ergebnis 16), dann kommt das raus:
(8÷2*2+8÷2*2)=X
(4*2+4*2)=X
(8+8)=X
16=X
Ist mir ein rätsel was an dieser Aufgabe diskutabel sein soll und wieso sowas viral geht. Es gibt nur das eine Ergebnis 16 und darüber nach meinem mathematischen Schulwissen auch keine Diskussion über das herbeiführen dessen
Den Artikel kann man mathematisch gesehen direkt in den Mülleimer werfen. Wie bereits erklärt wurde, ist die Rheienfolge bei Faktoren komplett egal.
Wenn man aber anstelle von einem “ : “ einen Bruchstrich schreibt (was grundsätzlich viel geordneter und praktischer ist), ist die Lösung eindeutig 1. Mit einem “ : “ sieht die Aufgabe dann so aus:
8:(2(2+2))
Und das ergibt ganz klar 1. Die richtige, und einzig richtige Lösung lautet also 1.
@Momo Die Reihenfolge ist nicht egal wenn ein Faktor teil eines Bruch oder einer Division ist. Zudem sieht es mit Bruchstrich so aus:
8
— * (2+2) = 16
2
Vielen Dank, habe richtig Aggressionen bekommen als manche behaupteten das Ergebnis sei 1.
Das ist schlichtweg falsch.
Wäre eine große Klammer nach dem Bruch gesetzt (also 8/(2*(2+2)) ), dann wäre die einzig richtige Lösung 1.
Da dem aber nicht so ist, ist die einzig richtige Lösung 16 (stupide Klammer geht vor, danach von links nach rechts)
Also kein Spielraum für Diskussionen.
Dass die erste Lösung falsch ist, ist kompletter Quatsch. Beide Lösungen sind gleichermaßen richtig. Es hängt alles daran, dass „/“ kein eindeutig dargestellter Bruch ist. Je nach Interpretation ist die Klammer Teil des Nenners oder eben nicht – und Jeder, der das anders sieht, der übersieht oder ignoriert die Tatsache, die ich gerade vorher festgestellt habe.
EDIT: Und nein, wie es zu interpretieren ist ist NICHT standardisiert. Es ist eine Schreibweise, die die wohldefinierte Mathematik an sich überhaupt nicht erlaubt.
8/2+3(2+2) ist übrigens auch 16 Das ist doch eine ganz klare Punkt vor strich und Klammer zuerst Rechnung, verstehe nicht warum es hier Uneinigkeit gibt.
Meine Meinung dazu (Mathematiker hier): Die Aufgabe ist Schwachsinn und bekommt mehr Aufmerksamkeit, als sie verdient. Der Divisionsoperator „:“ kommt jenseits der Grundschule nicht vor. In abgesetzten Formeln schreibt man einen Bruchstrich. Wo der Platz das nicht hergibt, z.B. in eingebetteten Formeln, schreibt man einen Querstrich „/“. Natürlich entsteht die Verwirrung erst, weil der Faktor 4 als Summe (2+2) geschrieben ist. Das eröffnet die Option, den Multiplikationspunkt wegzulassen. Angenommen, wir hätten in einem Text 1/2x. Was ist das? Niemand würde das so schreiben, jedes Fachjournal würde eine solch unklare Notation zurückweisen. Entweder man schreibt (1/2)x oder 1/(2x). Nichts anderes ist akzeptabel.
Sich auf die dämliche von-links-nach-rechts-Regel zu berufen, hat nichts mit Mathematik zu tun. Die Mathematik ist abstrakt und steckt unter den Formeln, dementsprechend ist dies hier nicht eine Matheaufgabe. Die polnische Notation ist genause mathematisch. Wer sich dem Sophismus „Mathematik ist keine Ansichtssache“ hingibt, hat offenbar auch keine Mathematik gesehen. Über Konventionen darf man streiten und sich auch hinwegsetzen. Ist Null eine natürliche Zahl? Die DIN hat dazu eine Meinung (ja), die Mehrheit der Mathematiker behandelt die natürlichen Zahlen jedoch als bei Eins anfangend und verwenden ansonsten die gesonderte Notation N_0. Wichtig ist, dass man die in der eigenen Arbeit verwendeten Konventionen ordentlich kommuniziert. Auch der verantwortungsvolle Umgang mit Typografie gehört dazu. Das wurde bei dieser so genannten „Matheaufgabe“ jedoch verletzt: Wenn man 8 : 2(2 + 2) schreibt und (8/2)(2+2) meint, suggeriert man durch die Abstandsverhältnisse eine höhere Bindung als beabsichtigt ist. Es ist entweder zu klammern oder zumindest ein Leerraum zu setzen, 8/2 (2+2), damit man durch die Abstandsverhältnisse nicht fälschlicherweise eine höhere Bindung vortäuscht.
Da wird einem ja himmelangst wenn Menschen meinen 1 wäre die richtige Lösung! Hoffentlich haben diese einen Job, der gänzlich ohne Mathematik auskommt. Ich sage dazu nur: http://cpp.sh/8xv7h
Jedes Ergebnis, dass nicht 1 ist, ist fachlich falsch, nach amerikanischen/werstlichen Vorbild geprägt.
Der „billige“ Grundsatz, von rechts nach links zu rechnen, ist die allerletze Option, die man nehmen kann.
Der fachlich korrekte Losungsweg sieht so aus:
Zuerst wird die Klammer aufgelöst. Also aus 8÷2(2+2), wird 8÷2(4).
Danach wird DIE HANDLUNG MIT DER KAMMER ausgelöst, also aus 8÷2(4) wird letztenden Endes 8÷ (2×4) = 1
Anders betrachtet, rein aus mathematischer Sicht, kann man noch mit Variablen experimentieren:
y1 (Ergebnis) ist „1“, oder y2 ist „16“ – diese beiden Ergebnisse sind die, die als plausibel gelten, wobei eine davon korrekter ist als die andere.
Grundsätzlich liegt ja das Problem bei der vor der Klammer gesetzten „2“.
Ersetzen wir also jene durch ein „x“ und nehem jeweils y1 als auch y2 als Ergebnisse:
Zuerst: y1: 1 = 8 ÷ x(2+2)
Dann: 1= 8 ÷ x(4)
AB HIER tritt die Problematik auf, denn mit y2 wäre es ja jetzt so: 16 = 8 ÷ x(4), sodass um x = 2 (das was wir suchen) zu kommen, muss man
16 = (8÷x) × 4 aufgelöst nach 4x = 8 x = 2
Wer würde aber so „(8÷x) × 4 „rechnen? Das ist eine Entartung der Mathematik, einer absolut logischen und korrekten Wissenschaft!
Die einzige, vernünftige Losung wäre 8 ÷ 4× bei y1 = 1 zu rechnen und dann nach x auslösen
1 = 8 ÷ 4x /×4x
4x = 8 /÷4
x = 2
Somit ist die Lösung der Aufgabe „1“
Vielen Dank für den Zeitaufwand beim Durchlesen.
Komisch, mit meinem Schulwissen aus der DDR gibt es klar nur eine Lösung: 16. Vor der Punktrechnung kommt immer noch die Klammerrechnung.
wer keine Ahnung von Mathe hat, kommt sogar sicher noch auf mehr Lösungen
Fakt ist: es gibt nur eine (und das sollte jemand mit Grundschulausbildung verstehen)
@Jens vom GoogleWatchBlog
Sechs setzen!
Term 1 = 8
Term 2 = 2(2+2)
Das Schöne daran ist, dass durch weitere Klammern um Term 2 das Ergebis 1 ist und das ist richtig!
Was ist das für ein Schwachsinn hier, die Einserleute denken sich einfach eine Klammer aus und schreiben dif komplette Aufgabe unter einem Bruchstrich. Wenn ich die Hälfte dazu erfinde kann ich jedes Ergebnis daraus bauen. Aber 5+5+4/2+2(2+2) kann ich doch nicht einfach alles hinter der Division unter einen Bruch schreiben, dass ist absoluter Schwachsinn und einfach etwas dazu erfunden was gar nicht da ist. Das ist eine ganz simple punkt vor Strich rechen Aufgabe, wobei jeder wissen sollte, dass der Inhalt der Klammer noch vor allen anderen in der Aufgabe kommt. Unfassbar wie man so umständlich denken kann, nur weil man Recht haben will denkt man sich einfach was dazu, was gar nicht da ist, nirgends in der Aufgabe wird angezeigt, dass nach der 8 alles unter einen Bruchstrich steht Ich kann gar nicht fassen, dass man über sowas tatsächlich eine Diskussion führen muss, so viele Leute ohne Verstand.
Punkt vor Strich — Genau, und nicht
anders, mit aller Konsequenz!
es ist traurig mitanzusehen, dass es so sture Leute gibt und es einfach nicht wahrhaben wollen: BITTE SCHLAGT EURE MATHEBÜCHER AUF UND LEST NACH, WIE MAN EINS-UND-EINS RECHNET. Natürlich ist die gesamte community in diese zwei Lager (1 und 16) gespalten. In die, die sich auskennen und die, die es nicht tun!
8 / 2 × (2+2) = 8 / 2 × 4 = 8 × 1/2 × 4 = 4 × 4 = 16
8 / (2 × (2+2)) = 8 × 1/(2×4) = 8 × 1/8 = 1
… wie man sich leicht überzeugen kann, steht zweiteres aber nicht in der Angabe …
Bei der „Matheaufgabe“ musste man 8 geteilt durch …. lesen! Das ergibt 1
Liest man jedoch 8 Halbe mal …. wäre das Ergebnis 16!
Das muss man nicht verstehen, man muss es richtig lesen!
Und zum Dritten! 1 ist richtig!
8 halbe? was laberst du für ein müll du nimmst 8 geteilt durch 2 dass ist 4 dann mal 4 weil die Klammer wirst selbst du noch in der Lage sein zu errechnen und dann hast du 4 mal 4 was für dich wahrscheinlich schwer ist, kommt aber 16 raus. Nirgendwo in der Aufgabe steht das 2(2+2) komplett so unter einem Bruchstrich steht. Ihr denkt euch das einfach nur aus, dass es unter dem Bruch steht aber in der Aufgabe geht nicht hervor das alles in einem Bruch steht, theoretisch ist gar kein Bruch vorhanden. Das geteilt ist einfach ein Zeichen wie +,-,*, was soll der Schwachsinn. Nur weil ein geteilt dort steht schreibt man doch nicht komplett alles unter einen Bruchstrich. Ist wirklich unfassbar was es für Menschen gibt.

Würde es heißen 2+2/2+2+3+4-5+6 schreibt man natürlich den Teil 2+2+3+4-5+6 komplett unter einem Bruch, ne ist klar, weil ihr zu blöde seid einfach 2geteilt durch 2 wegen Punkt vor Strichrechnung als erstes, haut man einfach den kompletten Rest der Aufgabe unter einen Bruchstrich. Und wieso sollte man 2mal 4 vor 8/2 rechnen? Macht überhaupt keinen Sinn. Man löst einfach die Klammer auf und rechnet wie immer von links nach rechts und fängt nicht irgendwo in der Mitte an. Da fehlen einem echt die Worte, dass es so beschränkte Menschen gibt, kein Wunder, dass diese Welt den Bach runter geht, wenn man bei so einer bescheuerten Aufgabe schon nicht seine Fehler eingestehen kann, hoffe hier ist kein Arzt dabei, der auf 1 kommt, ansonsten sollte man die Patienten warnen, wenn die Leute ein Herz Problem haben dichtet der wahrscheinlich sonst noch ein Beinamputation dazu, damit das schwache Herz nicht so überanstrengt wird.
Da hast du deinen Bruchstrich,
Und mal etwas weniger ausfallenden werden. Oder sonst noch kein Erfolgserlebnis gehabt.
Symbole für die Division
Als Geteiltzeichen werden im Textsatz ein Doppelpunkt (:), ein Doppelpunkt mit Mittenstrich (÷) oder ein Schrägstrich (/) verwendet. Brüche werden durch einen Bruchstrich dargestellt, der im Textsatz dem Schrägstrich ähnelt. Im Formelsatz werden Zähler und Nenner eines Bruches übereinander dargestellt, mit dem nun waagerechten Bruchstrich als Trennlinie.
In den meisten Ländern, auch in Deutschland, wird in der Schulmathematik bevorzugt der Doppelpunkt (:) eingesetzt; im englischen Sprachraum und auf Taschenrechnern wird meist das Obelus-Zeichen (÷) verwendet. In der höheren Mathematik finden sich fast ausschließlich die Bruchschreibweise ( {\displaystyle {\tfrac {a}{b}}} {\tfrac {a}{b}}, selten auch {\displaystyle {}^{a}/_{b}} {}^{a}/_{b}) oder die Schreibweise als Multiplikation mit dem Kehrwert ( {\displaystyle ab^{-1}} ab^{{-1}}), die insbesondere bei nicht-kommutativer Multiplikation die nötige Klarheit setzt. Der Schrägstrich (/) findet sich vor allem in Programmiersprachen.
Und ich sitze hier und denke, sowohl 1, als auch 16 ist richtig und gleichzeitig falsch
DonDominato, EHX und Jakob haben recht.
Jakob hat es sehr schön gesagt: Das hier ist keine Matheaufgabe!
Mathematisch gibt es natürlich eindeutige Regeln, aber bei der Schreibweise leider nicht.
Alleine schon wenn ich den Doppelpunkt als Divisionsoperator sehe, kommt es mir kalt hoch.
Diese Schreibweise ist einfach nur Käse.
Hätte ich sowas in meinen Arbeiten geschrieben, mein Professor hätte mich mit der Arbeit verdroschen.
Also jeder Taschenrechner ist in der Lage dies auszurechnen und auch in der schreibweise und das Ergebnis ist immer 16. Ich habe aber jetzt auch keine Lust mehr hier weiter zu diskutieren, ich hoffe nur für euch, dass ihr nicht wirklich so blöde seid und bloß etwas Aufmerksamkeit erhaschen wolltet, und hoffe das keine Leben von euch abhängig sind. Schönen Tag noch * Mic drop*
Der große Fehler, den da die meisten machen, ist der, daß 2(4) NICHT das selbe ist wie 2 . 4!!!!!! Bei 2(4) ist das eine Einheit (man könnte auch schreiben [2(4)] !!! ), die ZUERST aufgelöst bzw. berechnet werden MUSS!!!!!! Und daher darf ich auch nicht die Division durch 2 vorher ausführen! Daher bleibt nur 8 : 2(4) = 8 : 8 = 1.
Das BODMAS-Prinzip sagt eindeutig aus, daß ALLE Klammern ZUERST ausgerechnet werden müssen!!!!! Also auch 2(4).
moin, schon mal etwas vom Kommutativgesetz gehört?
Machen wir was ganz anderes: du hast 8 Äpfel und ein paar Leute, wieviele Äpfel kriegt jeder?
Da wäre ein Auto, da sitzen 2 Leute vorn und 2 Leute hinten drin. Und dann steht da noch so ein Auto. Also 2 Auto mit (2 + 2) Leuten. Und von denen kriegt jetzt jeder 16 Äpfel?????? Kann ich mir nicht vorstellen, weil ja nur 8 da sind.
Gegenvorschlag?
Wie wäre es damit: Du siehst 8 Äpfel vor dir und 2 Leute daneben. Links, rechts und hinter dir die gleiche Situation. Wieviele Äpfel darf jeder nehmen? Ha, es ist weder 1 noch 16, die Lösung ist 4!
Was lernen wir daraus? Nicht einfach wahllos Einheiten dazu erfinden!
Oh, die wundersame Vermehrung hat stattgefunden! 8 Äpfel, 2 Leute daneben, 2 rechts, 2 links, 2 hinten – und jeder bekommt 4 Äpfel! Geht das mit Geld auch????
Es gibt in der Aufgabe weder Äpfel noch Personen, wenn man die einfach dazu erfindet kommt natürlich Quatsch raus. Je nachdem was man zu was macht halt anderer Quatsch. Mit Mathe hat das dann nicht mehr viel zu tun.
Ein Argument (welches ich benutze ) hab ich bis jetzt noch nicht gelesen:
) hab ich bis jetzt noch nicht gelesen:
Der term 2(2+2) ist zwar eine multiplikation, aber meines erachtens, wie 2(a+b), bindet man die multiplikation implizit an die 2 uns nicht an die 8.
Wenn man die Rechnung durch variablen ersetzt a/b(c+d) würe man es ganz klar in a/(bc+bd) umrechnen, dann die zahlen einfügen 8/ (2*2+2*2) = 8/ (4+4) = 8/8 = 1.
Um auf 16 zu kommen müsste man doch streng genommen das multiplikatorzeichen eindeutig hinschreiben, da sonst die multiplikation des Werts in der Klammer implizit and die 2 gebunden ist. Oder nicht?
Ich sehe schon, jede existierende Tabellenkalkulation und jeder Taschenrechner, mit dem ich in meinem Leben gerechnet habe, haben einen schwerwiegenden Bug! Ich muss großes Glück gehabt haben, dass ich überhaupt Schule und Studium geschafft habe. Nicht zu fassen…
Was ist mit Regel der klammern Auflösung
a(b+c) = ab + ac